Машина Тьюринга

Программные инструменты богаты и многочисленны, а аппаратное обеспечение мощное и дешевое. Один простой способ измерить постоянно растущую сложность и изощренность программных инструментов — посмотреть, что требуется для создания «Hello, world!» программа. На заре C и Unix™ для этого требовалось всего несколько строк исходного кода. Теперь, используя компилятор Windows C/C++ или другой инструмент программирования с графическим интерфейсом, даже создание простой программы «hello world» требует сотен строк вспомогательного кода, который программист приложения редко видит. Среды программирования могут быть большими, потому что доступные сегодня машины становятся мощнее по мере того, как падают в цене. Инструменты становятся проще в использовании, а отладчики усложняются. Сейчас хорошее время для программистов, но иногда мы ослеплены мощью и элегантностью наших программных инструментов и аппаратных платформ.

Иногда стоит сделать шаг назад и посмотреть на мир с точки зрения первых принципов. Физики (по крайней мере, хорошие) смотрят на мир из первых принципов. В математике первые принципы называются аксиомами. Приятно отвлечься от повседневной рутины запуска программ и думать о компьютерах с точки зрения аксиом. Какое отношение аксиомы имеют к написанию компьютерных программ? Попробуйте ответить на этот простой вопрос: что такое вычисление?

Что такое вычисление?
Ответ таков: последовательность конфигураций машины Тьюринга, приводящая к остановке, называется вычислением. Это означает, что если ваш алгоритм успешно работает на машине Тьюринга, это вычисление. Если это не так, то это не вычисление!

Мир, каким мы его знаем, изменился в 1936 году. В том же году, когда плотина Гувера начала генерировать электроэнергию, а Ширли Темпл стала самой кассовой, 24-летний англичанин по имени Алан Тьюринг написал статью под названием «О вычислимых числах». приложение к проблеме Entsheidungs.

Entsheidungsproblem — это немецкое выражение вопроса о разрешимости. 

Что такое Разрешимость?
Разрешимость означает: «Можно ли разработать алгоритм для решения конкретной проблемы, который дает ответ «да» или «нет»?

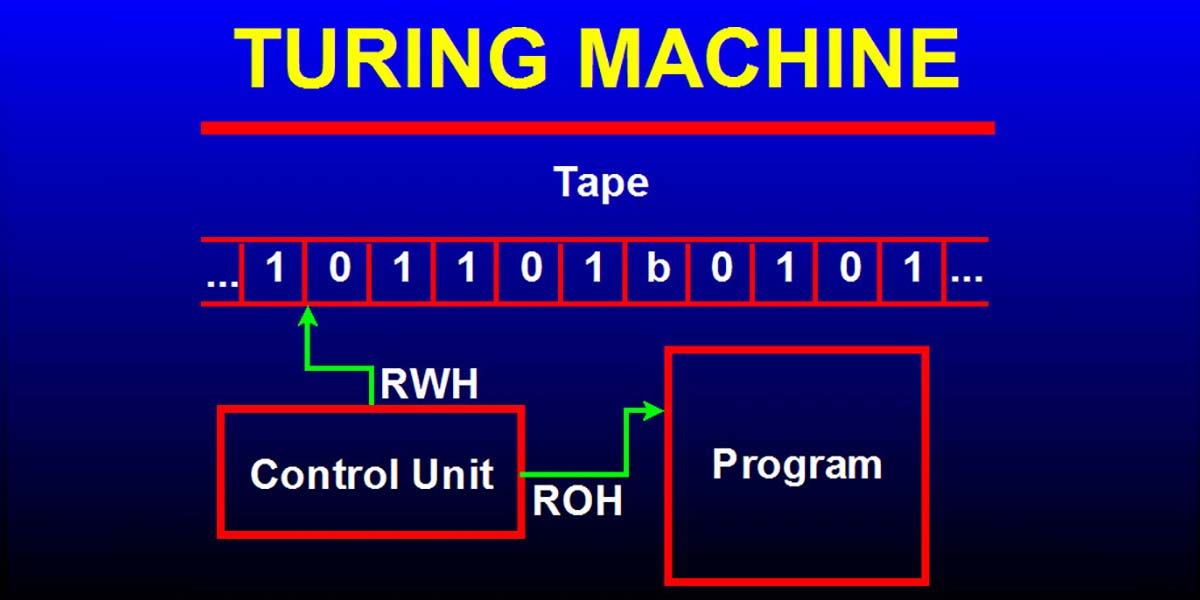
Почему такая вонь по поводу разрешимости? Начиная с 1910 года и до 1913 года Альфред Норт Уайтхед и Бертран Рассел опубликовали то, что считается одной из основополагающих математических работ, Principia Mathematica. В этом трехтомнике Уайтхед и Рассел попытались свести всю математику к подмножеству формальной логики. Они намеревались показать, что математика полна. Смысл слова «полный» в этом контексте означает, что доказательство или формула могут быть получены каким-то механическим способом. Из заведомо истинной аксиомы к механистическому алгоритму могут быть добавлены другие детали и условия для создания новых доказательств. Это мировоззрение, как и в ньютоновской физике, предлагает детерминистский взгляд на мир как на заводе. В 1931 году появился Курт Гедель со своей теоремой о неполноте. что эффективно показало, что основные понятия, которые мы считаем математическими истинами, не могут быть формально доказаны. Эта неполнота распространяется даже на простые числа. Это разрушило концепцию Уайтхеда и Рассела по вытачиванию механистических доказательств, что, в свою очередь, потрясло самые основы математики. Как может что-то быть разрешимым, если фундамент, на котором строится вопрос, неполный? В своей малоизвестной статье Тьюринг описал абстрактную универсальную вычислительную машину, которая теперь называется машиной Тьюринга. Как оказалось, нет более мощной машины, теоретической или реальной, которая могла бы сравниться по возможностям с машиной Тьюринга. Машина Тьюринга лежит в основе современной компьютерной науки. Абстрактная машина Тьюринга, как он настаивал с самого начала, действительно может быть построена. К сожалению, 1936 год был также годом, когда 4000 нацистских войск незаметно проникли в Рейнскую область и заняли демилитаризованную зону, продиктованную Версальским договором, что предвещало начало Второй мировой войны. В 1940 году, когда Англия находилась в состоянии войны, а немецкие подводные лодки безжалостно уничтожали конвои, Тьюринг (и другие талантливые математики) были призваны британским командованием для помощи в расшифровке немецких военных кодов. К счастью, секретная немецкая шифровальная машина под названием «Энигма» была захвачена с тонущей подводной лодки. С дополнительным бонусом в виде захваченной «Энигмы» Тьюринг взломал якобы неподдающийся взлому код «Энигмы» и внес значительный вклад в победу союзников в войне в Северной Атлантике. Неблагоприятный эффект войны заключается в том, что она остановила разработку и материализацию универсальной машины Тьюринга. После Второй мировой войны началась своего рода гонка между Англией и Соединенными Штатами за создание первого цифрового компьютера. Англия создавала ACE (автоматическую вычислительную машину), а Соединенные Штаты создавали ENIAC (электронный числовой интегратор и калькулятор). Тьюринг находился на периферии проекта ACE, а не в центре разработки аппаратного обеспечения, поэтому он обратил свои мысли к таблицам инструкций или к тому, что мы сейчас называем программным обеспечением. Стандартная машина Тьюринга показана на рисунке 1 . Он состоит из головки чтения/записи и ленты бесконечной длины, которая может перемещаться вправо или влево по одному сегменту за раз. Головка чтения/записи считывает и записывает символы на ленту.

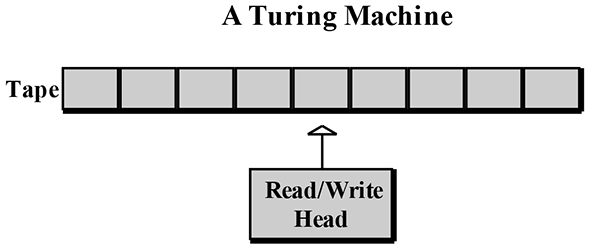
ФИГУРА 1.

Головка чтения/записи (иногда называемая управляющей головкой) может читать, записывать или стирать символ на сегменте ленты, в котором она находится в данный момент, но только по одному сегменту за раз. Хотите верьте, хотите нет, но этот простейший из простых компьютеров способен делать все то же, что и самый мощный суперкомпьютер. Рано или поздно, если вы будете изучать машины Тьюринга, вы столкнетесь с формальными обозначениями. Сначала это немного пугает, но это действительно полезно и легко понять. См. Рисунок 2 для объяснения символов машины Тьюринга.

ФИГУРА 2.

Формальное определение машины Тьюринга, обозначаемой как M, таково: M = (Q, Σ, Γ, δ, q0 , B, F).

Вот что это означает: Q — множество конечных состояний, Σ (сигма) — входной алфавит, Γ (гамма) — ленточный алфавит, δ (дельта) — функция перехода, B — пустой символ, q 0 — исходный алфавит. начальное состояние, а F — конечное состояние. Греческие буквы используются в качестве условного обозначения в теоретической информатике так же, как они используются в математике. Давайте рассмотрим пример, чтобы вы могли понять, как работает машина Тьюринга. Предположим, у нас есть лента, заполненная символами a и b и обрамленная пустым символом на каждом конце, как показано на рисунке 3 .

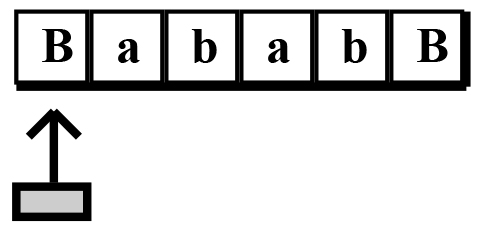
РИСУНОК 3.

 Мы установим начальную позицию под левым пробелом. Это начальное состояние q 0 . Мы хотим, чтобы машина Тьюринга заменяла каждое a на b и каждое b на a. Мы назовем эту машину Тьюринга обменником символов. Чтобы запрограммировать машину Тьюринга на обмен символами, нам нужно разработать набор правил или функций перехода δ. Вот правила на английском языке, а затем переведенные в символы машины Тьюринга: Начните с начального состояния, q 0 . Если пробел находится над считывающей головкой, повторно скопируйте пробел на ленту, установите новое состояние q 1 и переместите считывающую головку вправо. Символически мы можем записать это как (q 0 ,B) = {q 1 , B, R}. В общем случае это означает (State, Symbol) = {NewState, NewSymbol, MoveTo}. Используя символы, мы можем свести длинное словесное описание к короткому, точному символическому заявлению. В этом ценность того, чтобы потратить время на изучение символов и манипулирование ими. Что дальше? Теперь машина Тьюринга находится в состоянии q 1 , и теперь мы хотим, чтобы машина искала a или b и обменивалась ими, поэтому нам нужно больше функций перехода. Для состояния q 1 , если a над головкой чтения, оставайтесь в состоянии q 1 , запишите символ b на ленте и переместите головку вправо. Это переводится как (q 1 ,a) = {q 1 , b, R}. Если ab находится над считывающей головкой, оставайтесь в q 1 , запишите a на ленте и переместите головку вправо. Это переводится как (q 1 ,b) = {q 1 , a, R}. Чтобы заставить машину остановиться в конечном состоянии F, нам нужна еще одна функция перехода. Если пустой символ B находится над считывающей головкой, остановите машину Тьюринга. Это переводится как (q 1 ,B) = {F}. Эта функция перехода формально не определена при выполнении машины Тьюринга. Чтобы заставить машину Тьюринга остановиться, должен быть неопределенный переход, поэтому считывающая головка не может двигаться вправо или влево. Все функции перехода, описывающие машину Тьюринга, перечислены на рис. 4 . Каждый из наших переходов называется конфигурацией. Это последовательность конфигураций, которая вызывается на боковой панели. Что такое вычисление?

РИСУНОК 4.

Теперь нам нужно запустить машину Тьюринга, чтобы проверить, работает ли она. В большинстве классических книг по машинам Тьюринга переход от одного перехода к другому обозначается ( . Этот символ обозначает работающую машину Тьюринга. На рис. 5 показано как графическое, так и классическое представление нашей машины Тьюринга во время ее работы. Использование графического представления для машины Тьюринга любой сложности становится очень громоздким и занимает много места, поэтому вы вряд ли когда-нибудь их увидите. Вы почти всегда будете видеть классическое представление. Как вы можете видеть на рисунке 5 , считывающая головка обозначена функциями перехода q 0 и q 1 . Символ справа от считывающей головки считается символом под считывающей головкой. Когда считывающая головка считывает ленту, она перемещается вправо или влево и перезаписывает символ на ленте.

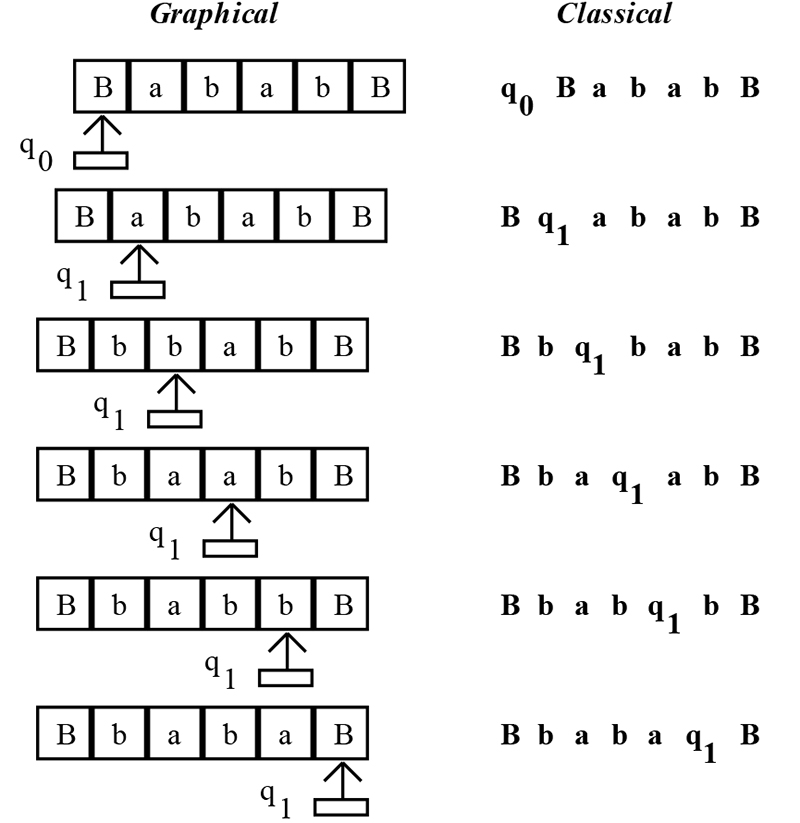
РИСУНОК 5.

Итак, мы показали, что наша машина Тьюринга, которая заменяет символ a на символ b, действительно работает. Так в чем же дело? Дело в том, что алгоритм преобразования одного символа в другой на самом деле является вычислением, и, поскольку он правильно работает на машине Тьюринга, он должен работать на любом мыслимом компьютере во вселенной! Вот насколько на самом деле глубока и глубока машина Тьюринга. А если сложить два числа вместе? Мы интуитивно знаем, что это действительно вычисление, но как вы это докажете? Посмотрите, работает ли он на машине Тьюринга! Одним из способов представления чисел на ленте является использование унарного формата. В унарном формате число два выражается как 0110. Три единицы используются для представления числа три, а нули используются для разделения чисел. Число пять является унарным форматом 0111110. Мы хотим увидеть, является ли два плюс два вычислением, поэтому лента будет выглядеть как B0110110B (не забывайте, что лента заполнена пробелами, поэтому у нас есть пустые символы, уходящие в бесконечность на оба конца ленты). Как мы можем создать машину Тьюринга для сложения этих двух унарных чисел? Посмотрите на ленту некоторое время. Результат, который нам нужен, равен четырем, или 011110. Если мы сможем сдвинуть крайние правые единицы на одну позицию влево, мы получим желаемый результат. Нам нужна форма сдвигового регистра. Удивительно, насколько машина Тьюринга эмулирует современный компьютер, а она была изобретена в 1936 году! На рис. 6 показаны функции перехода для сумматора и машина Тьюринга в действии с использованием классических обозначений. Запустите это через симулятор машины Тьюринга, чтобы проверить, как это работает.

РИСУНОК 6.

 Симулятор машины Тьюринга состоит из трех частей: входного файла ленты, файла функций перехода и симулятора tms.exe. Входной файл ленты представляет собой текстовый файл ASCII, содержащий символы ленты. Файл функции перехода использует формат, аналогичный классической форме машины Тьюринга. Комментарии также размещаются путем размещения буквы C в начале строки. Из-за несколько загадочной природы классической нотации машины Тьюринга свободное использование комментариев обычно необходимо (если вы хотите помнить, что вы сделали!). Элементарный синтаксический анализатор считывает переходы из исходного файла и загружает переходы в массив структур. На самом деле мы создали интерпретатор. Файл функции перехода — это исходный код программы, входной ленточный файл — это данные, а программа tms.exe — это интерпретатор. Процесс чтения файла исходного кода, разбиения исходного кода на отдельные символы или токены с последующим сохранением токенов в структуре данных называется синтаксическим анализом. Наш парсер находится в функции ReadTuringMachine(). Чтобы сократить длину кода, ReadTuringMachine() содержит небольшую проверку ошибок. Это означает, что файл функции перехода должен быть достаточно корректным, поскольку функция ReadTuringMachine() не обнаруживает синтаксических ошибок. Входные символы ленты загружаются в массив InputTape[MAX_TAPE_LEN]. Функции перехода загружаются в массив структур TURING_MACHINE. Структура TURING_MACHINE и ее связь с формальными функциями перехода показаны на рисунке 7 .

РИСУНОК 7.

Симулятор машины Тьюринга может работать в одношаговом режиме, который выполняет один переход за раз, или в автоматическом режиме, который выполняет все функции перехода на полной скорости. Входная лента, функции перехода и трассировка вычислений для обменника символов показаны на рисунке 8 .

РИСУНОК 8.

Надеюсь, эта статья познакомила вас с машинами Тьюринга. Разработанная здесь простая программа «Машина Тьюринга» является лишь отправной точкой. Существуют многоленточные машины Тьюринга, универсальные машины Тьюринга и многие другие варианты. Адаптация программы TMS для чтения нескольких лент была бы интересным проектом. Думать в терминах машин Тьюринга иногда может быть сложно и утомительно, но наградой является полученное понимание фундаментальной природы вычислений. Забавно писать машины Тьюринга и смотреть, как они работают на симуляторе. Попробуйте спроектировать машину Тьюринга для копирования строк или выполнения других основных арифметических операций, таких как вычитание или умножение. Некоторые машины создать легко, а некоторые чрезвычайно сложно. Попробуйте и посмотрите. Просто создайте входной файл ленты и файл функции перехода. Обычно я добавляю расширение .dat к файлам входных лент и расширение .tm к файлам функции перехода. Ограничений по именованию нет, поэтому, если хотите, используйте свою собственную систему. Хотите узнать больше? Существует множество веб-сайтов, содержащих подробную и интересную информацию о машинах Тьюринга, а также множество функций перехода, которые можно найти для запуска в симуляторе. Помните, что из всех наук информатика все еще находится в зачаточном состоянии. Предстоит сделать много важных открытий и решить большие проблемы. Великие открытия делаются в рамках первых принципов. Использование устройства первого принципа, такого как машина Тьюринга, может помочь в этом.

ЗАГРУЗКИ

TMS.zip скачать